Understanding What X*x*x Is Equal To: A Simple Guide
Have you ever seen "x*x*x" written down and wondered what it truly means, or why it pops up so often? It might seem like just a string of letters and symbols, but this simple mathematical expression, you know, holds a lot of significance. It's a way we talk about growth, space, and power in a very compact form. We see its ideas everywhere, from how objects fit together to how information spreads, more or less.
At its core, "x*x*x" is a fundamental concept in mathematics, a building block, if you will, for many more complex ideas. It's about taking a number or a value, represented by that little 'x', and multiplying it by itself not once, but twice more. This process, actually, gives us a very specific kind of result, one that has a unique feel and application.
This idea isn't just for math class, though. It helps us describe things in the real world, things that have depth and volume. It’s also a concept that, in a way, mirrors how we think about expansion and influence, even in the digital spaces we use every day, you know. Today, we'll explore what this expression means, why it matters, and where you might encounter it, just a little.
Table of Contents
- What Exactly Does x*x*x Mean?
- Why is x*x*x Important? Real-World Uses
- How to Calculate x*x*x
- Common Misconceptions About x*x*x
- Your Questions Answered About x*x*x
What Exactly Does x*x*x Mean?
When you see "x*x*x", it's a shorthand, really, for a very specific mathematical operation. It means you take a value, any number at all that 'x' stands for, and you multiply it by itself, and then multiply that result by 'x' one more time. This process, as a matter of fact, gives us what we call "x cubed" or "x to the third power."
The Basics of Exponents
This idea of multiplying a number by itself multiple times is called exponentiation. It’s a powerful tool, you know, for writing very long multiplication problems in a much shorter way. For example, if you had 2*2*2, writing it as 2³ (read as "2 cubed") is much neater, isn't it? The little number up high, the '3' in this case, is called the exponent, and it tells you how many times to use the base number, which is 'x' here, in the multiplication. So, x*x*x is simply x with a small '3' as its exponent, like x³.
The base, 'x', can be any number: a whole number, a fraction, a decimal, or even a negative number. The exponent, on the other hand, tells you the "power" to which the base is raised. So, a number to the first power is just itself (x¹ = x), and a number to the second power is x*x (x²), which we often call "x squared." The third power, x*x*x, then, is the next step in this progression, expanding the idea even further.
Visualizing the Third Dimension: Cubes
The term "cubed" isn't just a fancy math word; it actually has a very visual meaning. Think about a physical cube, like a sugar cube or a dice. A cube has three dimensions: length, width, and height. If each of those dimensions is equal to 'x', then the volume of that cube is calculated by multiplying its length by its width by its height. So, it's x * x * x. This, arguably, is why we call it "x cubed."
This connection to a three-dimensional shape helps us understand the concept in a very tangible way. When you calculate x*x*x, you're essentially figuring out how much space a cube with sides of length 'x' would take up. It's a pretty neat way, you know, to link abstract math to the physical world around us. So, for instance, if 'x' was 2 centimeters, a cube with sides of 2 cm would have a volume of 2*2*2, which is 8 cubic centimeters, you see.
Why is x*x*x Important? Real-World Uses
The concept of x*x*x, or cubing a number, is much more than just a classroom exercise. It shows up in many different fields and helps us solve a lot of practical problems. It's a way of describing things that grow or expand in three directions, or simply have a significant impact, too.
In Science and Engineering
Scientists and engineers use the concept of cubing all the time. For example, when they need to calculate the volume of containers, tanks, or even the amount of material needed for a construction project, they often rely on formulas that involve cubing dimensions. Think about how much water a cubic meter can hold, or the space a specific chemical reaction might need. These calculations, basically, often come back to x*x*x.
In physics, for instance, the volume of a sphere is calculated using a formula that includes a cubed radius (r³). This is quite important for understanding everything from the size of planets to the behavior of tiny particles. Even in computer graphics, when designing 3D models or virtual environments, the calculations behind how objects appear and interact often involve three-dimensional math, where, you know, x*x*x ideas are fundamental.
Everyday Examples: Volume, Growth
Beyond the lab, you can spot the concept of cubing in many everyday situations. Whenever you think about the capacity of something – like how much liquid a box-shaped carton can hold, or the space inside a room – you're dealing with volume, which means you're often dealing with something akin to x*x*x. If a storage box has sides that are all the same length, say 'x' feet, its storage capacity is x³ cubic feet, so.
It also appears in ideas of growth, sometimes. While not always a direct x*x*x, the idea of something expanding in multiple directions, or having a magnified effect, can be related. Imagine how a small piece of information, like a trending topic on a social platform, can multiply its reach very quickly. This kind of exponential spread, in a way, echoes the power of cubing a number, showing a rapid increase in scale.
The 'X' Factor: From Algebra to Digital Platforms
The letter 'x' itself, as a symbol, often represents something unknown, a variable that can hold many possibilities, or even something vast and encompassing. This idea isn't just limited to algebra. For instance, the recent rebranding of Twitter to 'X' by Elon Musk, as described in "My text," shows how the letter 'X' is being used to represent a much broader concept – an "everything app." Musk's vision for 'X.com' into a "super app" is, basically, about expanding its utility and reach across many "dimensions" of digital life.
This transformation, you know, from a single-purpose platform to a multi-faceted one, is a bit like how x*x*x takes a single dimension and expands it into a three-dimensional concept. The 'X' in this context signifies a powerful, multi-layered digital town square, aiming to be a trusted global platform for everyone. Just as 'x' in mathematics can stand for any value and be cubed to represent volume or a higher power, the 'X' platform aims to encompass a wide range of services, expanding its 'power' and scope, you know.
Similarly, platforms like Zhihu, described as a "high-quality Q&A community and original content platform," and Reddit, a "network of communities where people can dive into their interests," show how digital spaces expand to offer diverse "dimensions" of interaction and knowledge sharing. They allow for an 'x' amount of individual interests to connect and grow into something much larger, a community, for example, or a shared body of knowledge. This expansion, then, is a bit like the conceptual growth we see when we cube a number.
How to Calculate x*x*x
Calculating x*x*x is pretty straightforward once you get the hang of it. It just involves repeated multiplication. You take your number, multiply it by itself, and then take that result and multiply it by the original number one last time. It’s actually quite simple.
Simple Examples
If x = 2:
2 * 2 * 2 = 4 * 2 = 8. So, 2³ is 8.
If x = 3:
3 * 3 * 3 = 9 * 3 = 27. So, 3³ is 27.
If x = 5:
5 * 5 * 5 = 25 * 5 = 125. So, 5³ is 125.
You can also cube fractions or decimals. For instance, if x = 0.5, then 0.5 * 0.5 * 0.5 = 0.25 * 0.5 = 0.125. It works the same way, just with different kinds of numbers, you see.
Tips for Larger Numbers
When 'x' is a larger number, doing the multiplication by hand can get a bit tedious. That's where calculators come in handy. Most scientific calculators have a dedicated button for exponents, often marked as xʸ or ^. You would typically enter your number, then press the exponent button, and then enter '3'. This makes calculating x*x*x for big numbers quick and easy, you know.
Even without a special button, you can just perform the multiplication steps one by one. For example, if you need to calculate 10*10*10, you'd first do 10*10 which is 100, and then 100*10 which is 1000. It's really just breaking it down into smaller, more manageable steps, that.
Common Misconceptions About x*x*x
It's pretty common for people to mix up x*x*x with other similar-looking expressions. Clearing up these little misunderstandings can really help solidify your grasp of the concept. So, let's look at a couple of them.
Not the Same as 3x
One of the most frequent mix-ups is confusing x*x*x with 3x. These are actually very different.
**x*x*x** (or x³): This means x multiplied by itself three times. For example, if x = 2, then x*x*x = 2*2*2 = 8.
**3x**: This means 3 multiplied by x. For example, if x = 2, then 3x = 3*2 = 6.
As you can see, the results are quite different. One involves repeated multiplication of the variable, while the other involves multiplying the variable by a constant number. It's a subtle but very important distinction, you know, in mathematics.
Negative Bases
Another area where people sometimes get confused is when 'x' is a negative number. When you cube a negative number, the result is always negative. Let's look at an example:
If x = -2:
(-2) * (-2) * (-2) = 4 * (-2) = -8. So, (-2)³ is -8.
This is because a negative number multiplied by a negative number gives a positive result, but then that positive result multiplied by another negative number brings it back to negative. This is, you know, a key rule to remember when working with negative numbers and exponents, too.
Your Questions Answered About x*x*x
We get a lot of questions about this topic, and it's good to clear up any lingering doubts. Here are some common questions people ask about x*x*x.
**Q: What does x cubed mean in simple terms?**
A: In simple terms, "x cubed" means you take a number, which we call 'x', and you multiply it by itself three times. Imagine you have a side length 'x' for a perfect cube shape. The total space inside that cube, its volume, would be x cubed. It's a way to show how much something grows when you expand it in three directions, like length, width, and height, you know.
**Q: How is x*x*x different from x squared?**
A: They are quite similar but represent different levels of multiplication. "x squared" (x²) means x multiplied by itself twice (x*x). Think of it as finding the area of a flat square with sides of length 'x'. "x cubed" (x³) means x multiplied by itself three times (x*x*x). This, on the other hand, is like finding the volume of a three-dimensional cube. So, x cubed adds another layer of multiplication and dimension compared to x squared, you see.
**Q: Where is x cubed commonly used outside of math class?**
A: You'll find x cubed used in many practical situations. Engineers use it to calculate the volume of materials, like concrete or water tanks. Scientists use it in physics, for example, when dealing with formulas for the volume of spheres or other 3D objects. Architects might use it when planning the space inside buildings. Even in everyday life, when you think about how much space something takes up, like a box or a room, you're dealing with a concept very much related to x cubed, you know. For more on exponents, you could check out Khan Academy's explanation of exponents.
We hope this has helped you get a better handle on what x*x*x is all about. It's a foundational concept that, actually, opens up doors to understanding so much more in math and the world around us. Learn more about mathematical concepts on our site, and link to this page for more advanced algebra topics.

x*x*x is Equal to | x*x*x equal to ? | Knowledge Glow
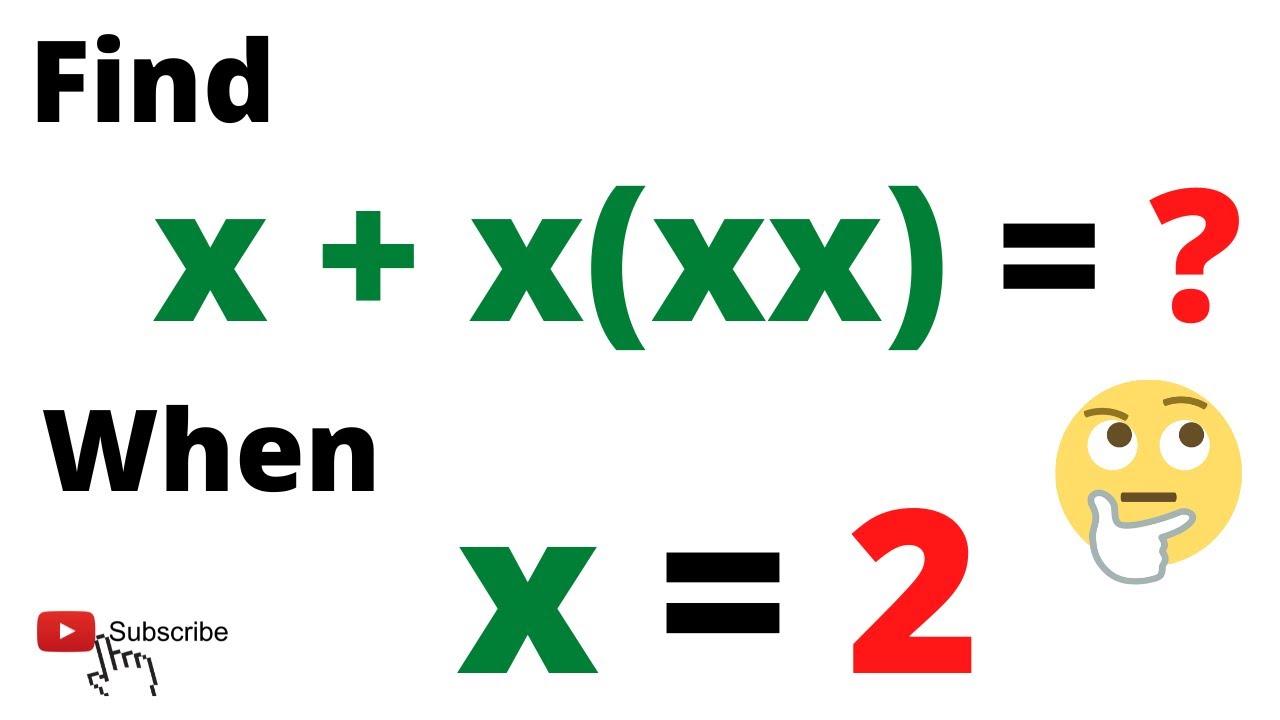
The value of x + x(xx) when x = 2 is: | Find the Answer in Seconds

X^X = 2^64 What Is X Equal To #maths #mathematics #math #mathematic