Unraveling X*x X*x Is Equal To 2023: A Look At The Math Behind The Numbers
There's something quite captivating, you know, about numbers and the puzzles they present. Sometimes, a simple-looking equation can spark a real journey of discovery. Like, what do you even do with something like x*x x*x is equal to 2023? It’s not just a string of characters; it's a doorway to exploring how math works, which is pretty cool, honestly.
This particular problem, x*x x*x is equal to 2023, might seem a bit unusual at first glance, right? It's like a little riddle that invites you to figure out what 'x' could possibly be. People, as a matter of fact, often come across these kinds of numeric questions and feel a pull to solve them, to find that precise answer that makes everything click into place.
We're going to take a careful look at this intriguing mathematical expression today. We'll break down what it means, how to approach finding the value of 'x', and even touch upon why such numerical quests can be so engaging for us. So, it's almost like a little adventure into the world of numbers, you know, to really understand this puzzle.
Table of Contents
- Understanding the Equation: x*x x*x is equal to 2023
- Deciphering the Challenge: Finding the Value of x
- The Allure of Numbers: Why Mathematical Puzzles Fascinate Us
- Exploring Exponents and Roots: A Closer Look
- The Number 2023: A Glimpse into its Traits
- Common Questions About Solving for x
Understanding the Equation: x*x x*x is equal to 2023
When you first see "x*x x*x is equal to 2023," it might look a little bit like a typo, perhaps, or maybe a very specific kind of code. But really, it’s a mathematical expression that uses multiplication in a repeated way. To make it clearer, we can write it in a more standard form, which is pretty helpful, you know, for solving it. The term 'x*x' means x multiplied by itself, which we usually show as x2. So, when you have 'x*x x*x', you're essentially multiplying x2 by x2. This, as a matter of fact, simplifies to x raised to the power of four, or x4.
So, the equation we're really looking at here is x4 = 2023. This way of writing it, you know, makes the problem much more approachable. It's a clear statement asking us to find a number 'x' that, when multiplied by itself four times, gives us 2023. This kind of setup is quite common in math, honestly, and understanding how to convert the initial wording into a standard equation is a really important first step.
The number 2023 itself is, well, just a number in this context, but it's also the recent past year for many of us. That connection, you know, sometimes makes these problems a little more interesting, a bit more grounded in our everyday lives. It gives a familiar touch to what could otherwise be a purely abstract mathematical exercise. So, in some respects, it's a number we've all lived through, which is kind of neat.
Thinking about 'x' in this way, as a variable in a power function, is something that comes up a lot. It's really different from, say, a logarithmic function like ln x, which behaves quite differently, especially as 'x' gets very small. Here, 'x' is just a base number that's getting multiplied by itself repeatedly, which is a very straightforward concept, actually. It's a fundamental part of how numbers grow or shrink in certain patterns.
Deciphering the Challenge: Finding the Value of x
Now that we understand our problem is x4 = 2023, the next logical step is figuring out how to find 'x'. When you have a number raised to a power and you want to get back to the original number, you use something called a root. Since 'x' is raised to the power of four, we need to find the fourth root of 2023. This is, you know, the inverse operation to raising something to the fourth power. It's like asking: what number, when multiplied by itself four times, gives us 2023?
Calculating a fourth root isn't something most of us can do in our heads, or even with just a simple calculator. You'd typically need a scientific calculator or, these days, a quick search on the internet. For instance, a tool like Wolfram Alpha can give you the precise answer. The fourth root of 2023 is approximately 6.702. So, if you were to multiply 6.702 by itself four times, you'd get a number very close to 2023.
It's important to remember, actually, that when you take an even root (like a square root, or a fourth root in this case), there are usually two possible answers: a positive one and a negative one. This is because a negative number multiplied by itself an even number of times results in a positive number. For example, (-2) * (-2) * (-2) * (-2) equals 16, just like 2 * 2 * 2 * 2 equals 16. So, for x4 = 2023, 'x' could be approximately +6.702 or -6.702. Both of these numbers, you know, work in the equation, which is pretty interesting.
This process of finding 'x' really highlights how different mathematical functions work. We're dealing with a power function here, where 'x' is the base. It's a straightforward concept, but it's quite fundamental. This is different from, say, a logarithmic function, where 'x' might be inside a log expression, like in ln x, which you might encounter in other kinds of problems. Those functions, as a matter of fact, behave in very different ways, and knowing the type of function you're working with helps you choose the right tools to solve it. This approach, you know, of isolating the variable, is a core skill in algebra, and it's something we use all the time, basically, when we're trying to figure things out.
The beauty of this problem is that it has a definite answer, even if it's not a whole number. It shows us that not all solutions are perfectly neat and tidy, and that's perfectly fine. We often deal with approximations in the real world, and math gives us the tools to handle those too. So, in some respects, it's a very practical lesson, you know, in how numbers actually behave.
The Allure of Numbers: Why Mathematical Puzzles Fascinate Us
There's something genuinely satisfying, you know, about tackling a mathematical puzzle and finally cracking it. It's not just about getting the right answer; it's about the process of thinking, of applying what you know, and of seeing the pieces come together. Problems like x*x x*x is equal to 2023, while perhaps simple for some, represent that universal human drive to understand and to solve. It's a bit like a detective story, honestly, but with numbers as the clues.
Numbers, in fact, are everywhere around us, shaping our world in ways we often don't even notice. From the pixels on your screen, which, as a matter of fact, are not always a simple 2x or 4x jump (like how 2K isn't exactly double 1080P pixels, but more like 1.7 times, and 4K is four times, as my text mentioned), to the complex algorithms that power our favorite online stores like Pinduoduo, numbers are the backbone. Understanding how to manipulate them, even in a basic equation, gives us a little glimpse into that bigger picture. It's pretty cool, if you think about it.
This fascination with problem-solving extends beyond just math class. When people run into an issue, say, like being mistakenly identified as underage on a platform, as mentioned in my text, they look for solutions. They might turn to communities like Zhihu, which is, you know, a place where people share knowledge and insights to help others find answers. The same mental approach, that drive to find a resolution, is at play whether you're solving for 'x' or trying to fix a tech problem. It's all about figuring things out, basically.
So, these mathematical challenges aren't just abstract exercises; they sharpen our minds and build our ability to think critically. They teach us patience, too, and the value of breaking down a big problem into smaller, more manageable steps. This is, you know, a skill that's incredibly useful in pretty much every area of life. It's a very foundational way of thinking, actually, that helps us navigate all sorts of situations, from buying an Xbox Series X/S to understanding complex AI models like Transformers, as my text also touches upon. It's all connected, in some respects.
Exploring Exponents and Roots: A Closer Look
Let's take a moment, you know, to really appreciate what exponents and roots are doing in our equation, x4 = 2023. An exponent tells you how many times to multiply a number by itself. So

x*x*x is Equal to | x*x*x equal to ? | Knowledge Glow

x*x*x is Equal to | x*x*x equal to ? | Knowledge Glow
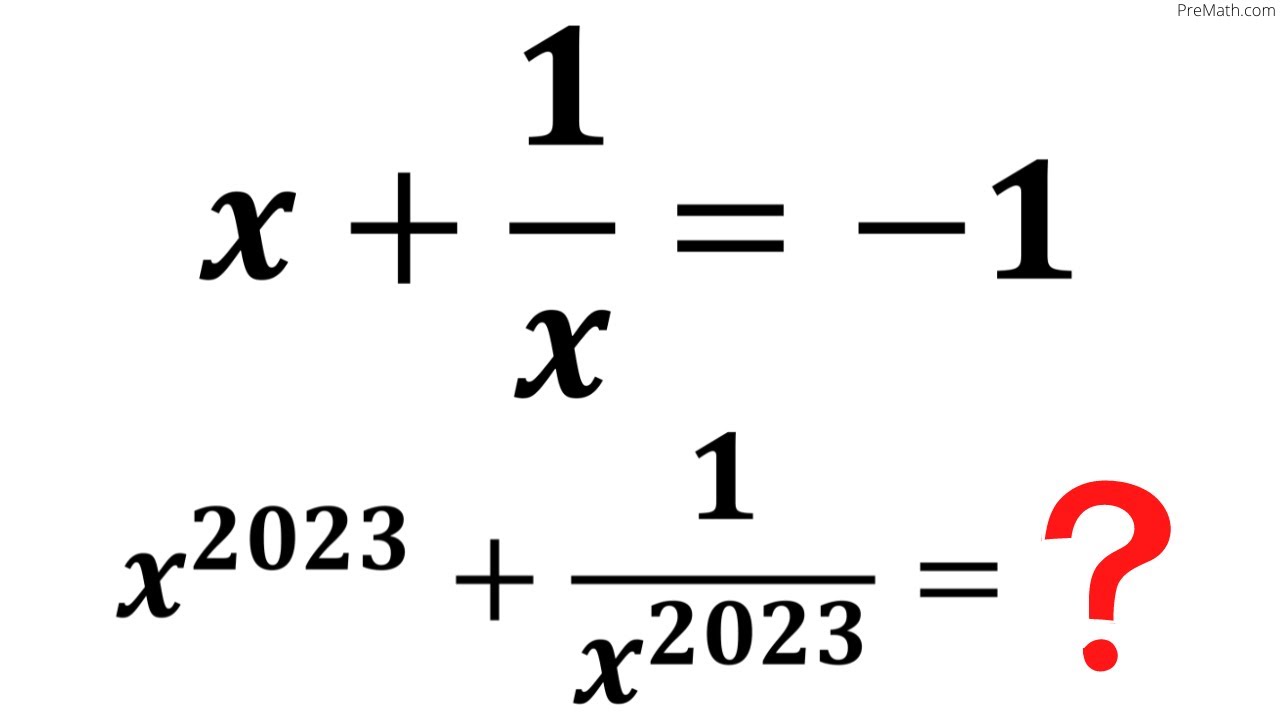
Olympiad Question | Learn to find the value of x^2023+(1/x^2023)| Math Olympiad Preparation